Support Vector Machine (SVM) is one of the machine learning’s classifier. Its goal is to find the optimal separating hyperplane which maximizes the margin of the data train. there are three important parts of this algorithm,namely the optimal separating hyperplane, the margin, and the data train. SVM will be implemented in a data train, so it is a supervised learning algorithm. this algorithm classifies the data into a certain class which makes it as a classification algorithm. To predict a class of a new data, SVM uses a hyperplane as the model that separates the classes and we can classify a new data just by looking at its position towards the hyperplane.
What Is Hyperplane?
we know
that the data train can be implemented in a space having any
dimensions. If we use a two-dimensional space, the hyperplane becomes a
line. If we use a three-dimensional space, it becomes a plane. And in more
dimensions, it becomes a hyperplane. So, a hyperplane is just a generalization
for a plane which the main task is to separate the data train into two classes.
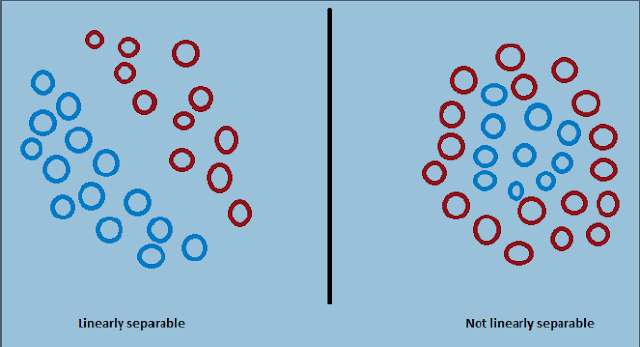
when we separate the data using a linear field (line, plane, etc), we can only
divide the data train into two classes in which in this case, we can say that
there are two categories of data,namely, positive
(1) and negative (-1). The
positive class can be presumed to be on the top of the hyperplane, and vice
versa for the negative class. Furthermore, since this
algorithm uses a linear field for the class division, it is clear that if we want to
separate the data train perfectly then there should be an enough space between
both classes that enables a linear field to separate them into the decent
position.The characteristic of this kind of the data train is called as linearly separable.
Simple illustration about the characteristics.
The Problems
From the above illustration,
we can see that there is a hyperplane located
arbitrarily which separates the data into two classes, one is above the line and
arbitrarily which separates the data into two classes, one is above the line and
the other is below the
line. However, there is an error for this model when we add
some data into the data
train.
Based on the
illustration, we can simply take a conclusion that it is not a good model of hyperplane when
it is located too close to data points of a class as there is a possibility that a
new data will go out of the scope of the hyperplane. So we need to enlarge the
distance from the data point to the hyperplane, yet the question is how do we
find the best distance?
To answer that question
is To find the margin of a hyperplane, we calculate the distance between the
hyperplane and the closest data point, double the value and we get the margin.
Here is an illustration of margin.
From the illustration,
it is clear that when we move the hyperplane to be closer to
the data point, then the
margin will be smaller and we’ve known that this is not a
good approach as it does
not anticipate the characteristic of the new data. So,
we can conclude that the
optimal hyperplane is the one that maximizes the
margin of the data train
in which it would be more consistent in receiving any new
data that has unpredictable
characteristic.
There are several
example of hyperplanes having different equation.
Based on the
illustration and the characteristic of an optimal hyperplane, our task
is to find a hyperplane
with certain equation and has the biggest margin.
How to compute the margin?
Before we compute the
margin, we need to know the equation of the hyperplane
as it’ll be used to
determine the position of the point in the hyperplane.
If we implement the SVM
on a two dimensional space, we’ll get a line as the
special representation
of the hyperplane in which the equation is y = ax + b.
Now, suppose we have two
vectors, namely w = (-b, -a, 1) and x =
(1, x, y). We
will prove that these
two vectors have a correlation with the line equation in which
if we can achieve that
point, then we’ll have two representations of the equation.
Afterwards, we’ll choose
the best equation representing the hyperplane based on
several considerations.
Here is an illustration
of the computation
Based on the above computation,
we can see that both equations represent the
will always perpendicular to the
hyperplane (normal vector). It is very
same thing, or in other
words we can say that we find another way to express the
line equation. The new
equation has two vectors as the variable representation
and it performs the dot product. For the equation of the
hyperplane, we will use
this new equation
because of these considerations:
helpful when we want to compute the
distance between a data point and the hyperplane.
Compute the Margin
We can see that the
vector w is perpendicular to the hyperplane and based on
the previous
explanation, we can get the vector’s component just by looking at
the coefficient of the
line equation (standard equation), namely w = (-b, -a, 1) if
the line equation is y - ax
- b = 0. From the above illustration we know that the
vector w can be
represented as (0, -3, 1), whereas the vector x is (1, x,
y). In this
case we can neglect the
first component (0) as it only determines the position of
the hyperplane relative
to the original point (0, 0).
Our task is to compute
the distance between the data point A and the hyperplane
or in other words we
will find the norm (magnitude of a vector) of the vector d.
Since the vector d is the
projection of the vector a onto the vector w, we can
apply this formula to
find the projection vector: d = (u.a)u.
After we have the
distance, simply double the value to get the margin.
That’s all for the
second part of this SVM’s tutorial. Next, we’ll see how to find the
optimal hyperplane when
we already had the margin.
Finding the Optimal Hyperplane
Let’s take a look at the
previous margin of the data train.
As we can see, it is not
the optimal hyperplane as intuitively, we can get the
bigger margin if we move
the hyperplane to the right. We can move it to the right
till it reaches a
certain position as if the position exceeds the limit, it will have a
new point of reference
and surely the created margin will be reduced.
Therefore, we will use
another approach in which we create two new
hyperplanes separating
the data and there is no any data point between them.
Afterwards, we create a
new hyperplane crossing the line representing the new
margin in the middle.
Here is the illustration.
From the above
illustration, we can see that the data point A and B become the
part of the hyperplane X
and Y respectively. We also see that the hyperplane Z
crosses the margin P in
the middle. By applying this approach, there are no data
points between the
limiting hyperplanes (X and Y) which means it makes the
margin of the data train
is created from the distance between the hyperplane and
any of two data points
reside on the limiting hyperplanes. Based on this
condition, this
hyperplane is considered as the optimal separating hyperplane.
Two and Three Dimensional Vector in the Equation of a Hyperplane
We’ve known that the
equation of a hyperplane can be represented in w.x = 0,
where w =
(-b, -a, 1) and x = (1, x, y). This representation is for three
dimensional vector, yet
there is another way to represent the equation of a
hyperplane, namely w.x + b
= 0. What is the difference between both equations?
We can see that we need
to add a b value to the latter equation
which means it is
a hyperplane’s equation
which is represented in a two dimensions vector space.
We can prove it by the
following procedure:
In this tutorial, we’ll
use the hyperplane’s equation having only two vector’s
elements.
The Constraints
Suppose we have a
hyperplane with this equation: w.x + b = 0. We also have the
limiting hyperplanes
which are represented in these equations respectively: w.x +
b = d and w.x + b
= -d. These equations state that the distance between the
limiting hyperplanes and
the optimal hyperplane is equal. However, we can
reduce the complexity of
the equation by replacing the value d with
one (it can be
any value and I use one
just for the simplicity).
The next step is we will
assure that there is no any data point between the
limiting hyperplanes and
we can utilize their equations to create the following
constraints:
From the constraints, we
can check whether a data point satisfies the rule. Let’s
take an example for the
data point A. We can see that this data
point resides
exactly in one of the
limiting hyperplane which means it satisfies the equation of
w.x + b = 1 or in
other words it’s just the equation of a line, namely y = ax
- b + 1
where -b + 1 is a
constant. The procedures to determine whether a data point
follows the rule is
still applied to another data point residing outside the limiting
hyperplane. If the
equation of w.x + b returns a value which is less that 1 and
more than -1, than the
data point does not satisfy the constraints and for this
case we will not choose
this kind of limiting hyperplanes to create the optimal
hyperplane.
Furthermore, we can get
a single constraint for the limiting hyperplane just by
combining both
constraints specified before. This single constraint will be used
as the equation for the
matter of optimization later.
The Margin
Let’s take a look at
this illustration.
As a reminder, our goal
is to find the optimal hyperplane in which it is the same
as finding the biggest
margin of the data train. If you recall again, we got the
optimal hyperplane by
creating the limiting hyperplanes where there are two data
points becoming a part
of them.
One of the approach to
find the value of the margin is by converting the margin M
to the vector
representation and then we can compute the norm of that vector. To
do the conversion, we
utilize the vector w as the base vector and the idea is we
get the vector M as the
result of the multiplication of the vector w by a
scalar.
Here
is the details of the process.
We’ve got the vector
representation for the margin and now we’ll see how to
compute the norm of the
margin by applying the vector in the equation of a
hyperplane.
The Optimization Problem
Finally, we’ve got the
way to compute the margin and according to the formula,
we can only change the
norm of w to get the maximum margin.
As we can see, when we
maximize the norm of w, the margin will become
smaller. So, our task is
to find the limiting hyperplanes that satisfies the constraint
and gives us the minimum
value for the norm of w.
To get the smallest
norm, we can use the single constraint which then gives us
this optimization
problem:
We have a couple (w,b)
and since the vector w can be represented as (-a,1),then
What we’re gonna do is
to manage the value of the gradient (a) so that the norm of w is minimum.
We can use the single
constraint for this problem:
Yi (w.xi + b) >=1
For any i=1,…, n
Conclusion:
According to me Support vector machine makes the model
efficient by tuning its parameters, Pros and Cons, and finally a problem to
solve. i would suggest you to use SVM and analyse the power of this model by
tuning the parameters. SVMs are really good for text classification. SVMs are
good at finding the best linear separator. The kernel trick makes SVMs
non-linear algorithms. Choosing an appropriate kernel is the key. For good SVM
and choosing the right kernel function is not easy. We need to be patient while
building SVMs on large datasets. i hope this Article is useful for you.




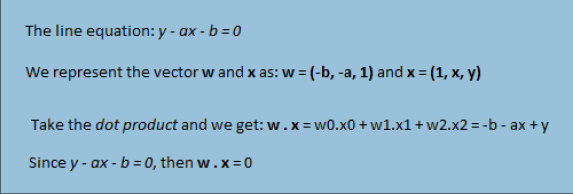












Comments
Post a Comment